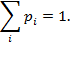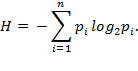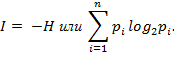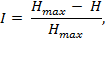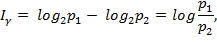| Главная » Статьи » Информационные основы cтратегического управления |
Термин "информация" давно и широко используется в науке, производстве и быту, но дать ему точное определение не так просто. Слово informatіо - латинского происхождения, и означает разъяснение, сообщение. Следовательно, в целом информация - это сведения о каком-то событии, деятельности, развитии определенного процесса, которые рассматриваются как результат передачи этих сведений от объекта к субъекту.
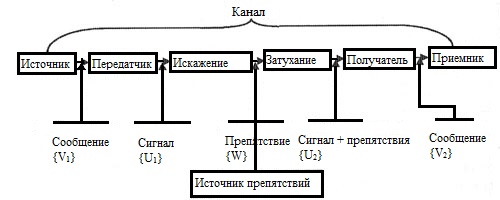
На бытовом уровне слово "информация" отождествляется с содержанием определенных сведений, которые могут иметь формы устного сообщения, листа, доклада, результатов определенных исследований, наблюдений и тому подобное. Точное определение информации, которым можно было бы всесторонне охватить ее качественное своеобразие, является затрудненным. Наиболее привлекательным является осознание того, что информация - это знания, которые получает субъект в результате восприятия и переработки определенных сведений. Норберт Винер отмечал, что информация - это обозначение содержания, полученного из внешнего мира в процессе нашего приспособления к нему. Кроме того, информация - это не материя и не энергия. Информация, в первую очередь, выступает как одно из основных понятий кибернетики, и принадлежат к начальным, неопределенным или аксиоматическим понятиям науки. Как отражение явлений реального мира, понятия информации раскрывается перечнем таких процедур: сбором, передачей, превращением и обеспечением пользователя достоверными сведениями. Как и все в природе, информация сочетает немало свойств, а, следовательно, нуждается выделения ее самых существенных характеристик. Информация по своей природе объективна. Она постоянно возникает в процессах, которые протекают в разных системах, и выражает качественную определенность или количественную меру свойств, взаимосвязей и взаимодействий между системами и элементами в системе. Информация, как и энергия, принадлежит к реальным и материальным процессам. Но особенность заключается в том, что отдаляясь от источника или объекта, который отображается, информация служит средством объяснения закономерностей реального мира и его превращения. В информационных процессах, как и в процессах труда, присутствуют три момента: собственно труд; предмет труда; средства труда. В материальном производстве предметы труда в процессе труда превращаются под действием средств и энергии в продукты труда. В процессах, связанных с информацией, предметом труда, продуктом труда и в определенной степени средствами труда выступает информация. А именно, в качестве предмета труда выступают начальные сведения о состоянии того или другого объекта, явления или процесса. Средствами переработки являются разные виды алгоритмов, а также технические средства превращения данных. В качестве продукта выступает результативная информация, которая является основой для принятия управленческого решения. С позиций кибернетики, информация выступает как мера устранения неопределенности. В ходе изучения информационных процессов были развитые подходы, которые связывают информацию с упорядочением материи и ее атрибутов с разнообразием материальных явлений, с неоднородностью материи и энергии. Отмечая многоаспектность термина "информация" следует учитывать, что она заключает в себе определенную логику развития теоретических взглядов, которые методологически интерпретируются на основе таких философских категорий, как единичное, особенное и всеобщее. Единичное, то есть, информация как сведения - сосуществует с особенным, то есть, с информацией, которая ликвидирует неопределенность и ведет к общему - к информации как неоднородности, упорядоченности, разнообразию. Информация является одним из центральных понятий кибернетики, таким же фундаментальным, как энергия для физики. В общем случае информацию можно рассматривать с трех точек зрения: технической; семантической (смысловой); результативной (эффективность информации), которые рассмотрим подробнее. С технической точки зрения важнейшей является точность передачи информации от отправителя к получателю. Эти проблемы рассматриваются в теории связи. Сюда же относится и количественная сторона передачи информации. Информативность данных здесь следует понимать как количество информации, которое содержится в этих данных и является важным свойством, которое определяет ценность данных. С позиций семантики, то есть смысловой трактовки информации, проблема заключается в сравнении содержания, которое было заложено в начальных данных отправителем, и содержании информации, которая передалась получателю. Данные воспринимаются получателем как информация в том случае, когда в его "памяти" заложено понятие и модели, которые позволяют понять содержание полученных сведений. Относительно результативности, то проблема в первую очередь заключается в эффективности полученной информации, то есть насколько полученное сообщение осуществило замысел или могло способствовать осуществлению желательного для получателя события. Например, сообщение о погоде осуществило определенное влияние или стало результативным для рыбалок, туристов, крестьян. Однако на людей, которые дома разыгрывают одну из шахматных партий, это сообщения ни одного влияния не осуществляет. Информация сама по себе не является материальной, но ее носители - материальны. Например, бумажные носители (книги, конспекты, листы, телеграммы и т. п.), токи, радиоволны и тому подобное имеют массу, вес, размеры и энергию. Но информация этих свойств не имеет. Ее можно получить, записать, запомнить, забыть, стереть или передать. Нельзя получить информацию оттуда, где ее нет. Вместе с тем, информация имеет такую характерность, как способность к распространению. Если, например, субъект получил новость, то есть определенную информацию, то скольким бы другим субъектам он ее не передавал, количество информации от этого не уменьшится, а во всех, кто ее получил, количество информации не превысит ее начального объема. При распространении информации ее общее количество не уменьшается, хоть в одних она увеличивается, а в тех, кто ее распространяет - не уменьшается. Понятие информации связано с динамическими процессами взаимодействия источника возникновения или передатчика информации и приемопередатчика. Сама передача осуществляется при наличии канала связи. Общая схема передачи информации изображена на рис. 11.1.
Рис. 11.1. Схема канала передачи информации В операторном виде передачу информации можно подать как последовательность операторов: A[{V1}]={U1}; B[{U1}+{W}]={U2}; C[{U2}]=C[B{U1}+{W}]={V2}. В этих выражениях A - оператор превращения сообщения V1 в сигнал U1. Он должен удовлетворить условие изоморфизма. Теория информации возникла как теория передачи данных и в начальной трактовке отождествлялась с теорией связи. В нынешней трактовке, кроме вопросов передачи сообщений, методы теории информации применяются в метрологии, нейрофизиологии, лингвистике, семиотике и других областях знаний. К важным проблемам, которые исследуются теорией информации, относится проблема эффективного использования каналов связи, их предельной пропускной способности и надежности, то есть способности доставлять информацию с минимальными потерями и искажениями. Понятие о количестве информации и возможности ее измерения является основой теории информации. Эти вопросы были разработаны американским инженером Шенноном в 1948 г. в статье "Математическая теория связи". С этого времени началось интенсивное становление теории информации и углубленное исследование вопросов об измерении ее количества. Однако это не значит, что к Шеннону не было попыток количественного измерения информации. Понятие о количественном соотношении между информацией и степенью упорядоченности системы в физике появилось в работах физика Больцмана (1872). Первые предложения об общих способах измерения количества информации были разработаны физиком Фишером при решении задач математической статистики. В рамках решения задач сохранения и передачи информации каналами связи вопросами определения количества информации занимались Найквист (1924) и Р. Хартли (1928). Общей чертой, свойственной для всех методов количественного измерения информации, является абстрагирование от содержания информации. Это, похоже, до того, что математика оперирует с количественными соотношениями, не удаваясь в суть и физическую природу тех объектов, которые стоят за этими соотношениями. Если абстрагироваться от семантики сообщений, то есть конкретного содержания тех событий, о которых передается информация, то отправным моментом для информационной оценки событий остается, лишь совокупность отличных одна от другой событий и, соответственно, сообщений о них. При передаче сообщений происходит их кодировка. При этом используется определенный алфавит, зная который, можно определить информационную вместимость системы, которая передает информацию и количество информации в сообщении. Один из подходов, который базируется на том, что алфавит сообщений имеет дискретный характер, был предложен Р. Хартли и носит название структурного. При его использовании берется к вниманию возможность получения от источника некоторого дискретного множества сообщений. Если количество возможных сообщений в этом множестве равняется N, то, за Хартли, количество информации I1, что приходится на одно сообщение, определяется логарифмом общего числа возможных сообщений N. I1=log2N. Если сообщения выходят от двух независимых источников, которые содержат N1 и N2 сообщений соответственно и передаются по одному каналу, то общее число возможных сложных сообщений от этих двух источников будет: N=N1 · N2, поскольку каждое сообщение от одного источника может быть объединено с каждым сообщением от второго источника. Поэтому количество информации, которая приходится на одно сообщение, будет таким: I1=log2N=log2N1·N2=log2N1+log2N2. (11.1) Следовательно, оказывается важное свойство логарифмической функции для определения меры информации, а именно - свойство аддитивности. То есть количество информации на сообщение равняется сумме количества информации, которые были бы получены на одно сообщение от двух источников, взятых отдельно. Следует отметить, что логарифмирование можно проводить при любой основе, но удобнее всего брать логарифм при основе 2. Недостаток структурного метода заключается в том, что при его использовании не учитывается разная вероятность поступления сообщений от источника. Поэтому приемлемее является статистический подход к определению количества информации. В его основу положено не только разное количество сообщений от источника, но и разная вероятность получения тех или других сообщений приемщиком. Такой подход был предложен Шенноном в 1948 г. Однако и этот подход не учитывает внутреннего содержания сообщений и их ценности для получателей. Очевидно, что большинство источников информации характеризуются неодинаковой вероятностью событий, что в них осуществляются, и, следовательно, неодинаковой вероятностью появления сообщений об этих событиях. Таким образом, выполнение тех или других опытов, связанных с этими событиями, носит черты большей или меньшей неопределенности. Степень этой неопределенности устанавливается вероятными характеристиками источника сообщений. Для сравнения подобных вероятных источников необходима числовая оценка степени неопределенности соответствующих исследований. Рассмотрим источники, в которых опыты имеют n равновероятных результатов. Будем считать, что неопределенность H результатов опытов зависит от количества возможных результатов, то есть H=f(n). Как указывалось выше, за функцию f целесообразно избрать логарифмическую функцию: H=f(n)=log2n. (11.2) Если n=2, то H=Iog22=l. В этом случае приходим к общепринятой единице измерения неопределенности, которая называется битом (bit), или двоичной единицей информации. Бит представляет собой неопределенность, которая содержится в одном исследовании, который имеет два равновероятных результата. Если говорить о n равновероятных результатов, то H=log2n=n 1/n log2n=n(-1/n log2 1/n), (11.3) но 1/n=p - это вероятность любого из n равновероятных результатов исследований. В этом случае: H=n(-plog2p) (11.4) Пусть некоторый опыт характеризуется таблицей вероятностей:
Понятно, что Тогда формулу (11.4) можно представить в виде: H = plog2p1 – p2log2p2 - … - pilog2pi - … - pnlog2pn =
(11.5) Последняя формула совпадает с выражением энтропии в статистической физике. Причем, это соотношение носит не только формальный, но и содержательный характер. Величина Н называется энтропией определенного опыта. Энтропия (от греч. - поворот, изменение, превращение) - это количественная мера неопределенности ситуации, или мера информации о состоянии системы, или количестве информации, которого не хватает для полной ликвидации неопределенности в системе. Энтропия рассматривается как количественная характеристика организованности систем. Мера информации, которая ликвидирует неорганизованность систем, и энтропия этой системы находятся в зависимости:
(11.6) Знак минус в формуле (11.6) перед Н не значит, что энтропия является отрицательной величиной. Поскольку 0<р< 1, а логарифм при основе 2 такого числа является всегда величиной отрицательной, то величина результата является величина положительна. Рассмотрим некоторые особенности энтропии. Энтропия - число положительное (в предельном случае Н=0). Энтропия определенного явления приближается к нулю, когда вероятность появления этого явления pi приближается к 1. Энтропия Н=0, если это явление однозначно определено. Максимум энтропии отвечает наибольшей неопределенности, то есть равенству вероятностей всех возможных явлений. Энтропия сложного опыта, в котором важный порядок результата и опыты α и β независимые между собой, определяется по формуле: H = (α,β) = H(α) + H(β). То есть энтропия сложного опыта равняется сумме энтропий независимых опытов. Количество информации или информационное содержание принятого сообщения определяется как разница между неопределенностью до принятия (Н) и после принятия сообщения: 1 = H – H1. Для определения информативности приемного сообщения используют зависимость:
где Hmax получается, когда pi = 1/n. Рассмотрен в предыдущем метод измерения количества информации полностью игнорирует ее содержание и корыстность для достижения цели, то есть ее ценность. Действительно, количество информации, которая определяется формулой (11.6), никоим образом не связано с содержательностью и корыстностью этой информации для пользователя. Формула дает возможность осуществить упрощенный структурный подход, который является характерным для таких технических систем, как телефон, факс, телеграф, компьютер, компьютерная сеть и т. п. Такой подход является оправданным с точки зрения секретаря-машинистки или телеграфистки, которые теряют время на печатание и передачу сообщений. Их интерес заключается в том, чтобы за единицу времени обработать большее количество символов. Относительно содержания того, которое печатается или передается, то их это вовсе не интересует. В практической деятельности людей интересует не столько формально-структурный подход к измерению количества информации, как содержание и практическая ценность полученной информации для конкретного пользователя. Во всех случаях, когда идет речь об информационных сообщениях, все они выражаются определенными знаками, словами, языком. При этом знаком называется условное изображение элемента сообщения. Слово выступает как совокупность знаков, которая имеет смысловое значение, а язык - это словарь и правила пользования им. Таким образом, рассуждая о количестве, содержании и ценности информации, нужно выходить из возможностей анализа знаковых структур. Этими вопросами занимается такая область знаний, как семиотика. Семиотику определяют как комплекс научных теорий, которые изучают разные свойства знаковых систем, то есть систем объектов разной природы, которые называются знаками, каждому из которых поставлено в соответствие некоторое значение. В таком понимании знаковыми системами есть обычные и искусственные языки, такие как языки программирования, информационные языки, логические, математические и химические символы и тому подобное. При рассмотрении семиотической проблематики выделяют три ее основных аспекты: синтаксис, семантику и прагматику. Синтаксис изучает способы соединения знаков и правила образования этих соединений и их превращений безотносительно к их значениям и функциям. Таким образом, рассмотренный нами структурный и статистический способы определения количества информации в сообщениях можно отнести к синтаксису. Семантика изучает знаковые системы как средства выражения определенного содержания и правила интерпретации знаков и их соединений, то есть изучает смысловую сторону языка. Прагматика рассматривает соотношение между знаковыми системами и их пользователями, или принимателями-интерпретаторами сообщений. Другими словами, к прагматике относится изучение практической корыстности знаков, слов и соответственно сообщений, то есть потребительской стороны языка. Семантический подход используется при определении количества информации. Методы количественного определения содержательного значения информации с позиций этого подхода еще достаточно не разработаны. Но есть рациональные подходы к решению этой проблемы. Вот, Р. Карнап и Бар-Хиллер предложили определять величину семантической информации через логическую вероятность. Она представляет собой меру подтверждения определенной гипотезы. При этом количество семантической информации растет в меру уменьшения степени подтверждения априорной гипотезы. Очевидно, что когда логическая вероятность равняется 1, то есть гипотеза построена на эмпирических данных, то количество семантической информации равняется нулю. И, наоборот, в меру уменьшения степени подтверждения гипотезы, то есть уменьшение априорного значения, количество семантической информации растет. Следовательно, мера семантической информации учитывает не только структуру и содержание самого сообщения, которое рассматривается, изолировано, но и запас знаний у получателя (пользователя) информации. То есть мера семантической информации указывает, какую новизну несет получателю сообщения по сравнению с тем, что он уже знал. Определение информационной содержательности сообщений основывается на учитывании "запаса знаний" приемопередатчика или пользователя информации. Необходимым условием их информативности и содержательности для пользователя является наличие у последнего определенного багажа знаний. То есть наличие определенного словаря, с помощью которого он может определенным образом интерпретировать полученные сообщения. Итак, можно утверждать, что семантическая информация одного и того же сообщения является неодинаковой для разных пользователей и зависит от уровня их знаний, или, как принято говорить, от их тезауруса. Тезаурус (от греч. - сокровище) в узком понятии - это словарь, в котором указаны не только значение отдельных слов, но и содержательные связи между ними, что служат для поиска слов определенного языка по их содержанию.
Прагматичный подход к определению количества информации. Из самого определения информации уже выплывает, что одним из свойств есть ее использование в процессе управления. А если так, то привычно ее оценить не только со структурно-статистической или семантической позиций, но и с позиции ее полезности, ценности и целесообразности для достижения поставленной цели. Каждое сообщение, которое получается системой управления, интересное не с точки зрения ее познавательных характеристик, а с точки зрения прагматичности, то есть полезности и ценности выполняемых функций управления (Прагма - от греч. - действие, практика). Исходя из этого, меру ценности информации можно определить как изменение вероятности достижения цели при получении информации. В этом случае мера ценности информации будет определяться по формуле:
где p1 - вероятность достижения цели к получению информации; p2 - вероятность достижения цели по получении информации. При этом возможны три таких случая. Полученная информация не может изменить вероятность достижения цели: в этом случае p1=p2, тогда Iγ=0 и такая информация называется пустой. p1 > p2, тогда p1 < p2, тогда | |||||||||||||||
| Категория: Информационные основы cтратегического управления | Добавил: | |||||||||||||||
| Просмотров: 5077 | Комментарии: 1 | |||||||||||||||